ドイツの顕微鏡学者JDMöllerによって作成された藻類の複雑なパターンである彼の最初の珪藻の配置を見て以来、マシュー・キリップはビクトリア朝の芸術に魅了されてきました。 「人間の手が自然の作品をとても美しく見せているのが大好きです」と彼は言います。
ほとんどすぐに、英国の映画製作者は2つの質問をしました。 最初に、これらの19世紀のアーティストは、それぞれわずか数ミクロンの珪藻を、肉眼では見えない眩しい形にどのように組み立てましたか？ 第二に、この媒体でまだ働いている人はいますか？
Killipが答えを探した結果、彼は唯一の生きた開業医であるKlaus Kempになりました。 彼はエキセントリックなイギリス人と午後を過ごし、カメラを転がし、上記の「The Diatomist」と呼ばれるドキュメンタリーを制作しました。 短編映画は今週公開されました。
この失われた芸術の詳細を知るために、私はメールでキリップにインタビューしました。
珪藻とは正確には何ですか？
珪藻は、美しいガラス殻に収容された微細な単細胞藻類です。 数十万種類の珪藻があり、それらはすべて独特の形をしています。
では、珪藻の配置はいつどのように芸術の形として現れたのでしょうか？
最初の珪藻の配置は1800年代初期にさかのぼりますが、芸術の形は世紀の後半にピークに達しました。 自然界に強い関心が寄せられた時期であり、芸術と科学がより密接に連携した時代でもありました。 珪藻の配置は、世界に秩序をもたらし、自然を合理的に表示したいという特にビクトリア朝の欲望の素晴らしい例です。
（ウィムヴァンエグモンド） 
（クラウス・ケンプ） 
（スパイクウォーカー） 
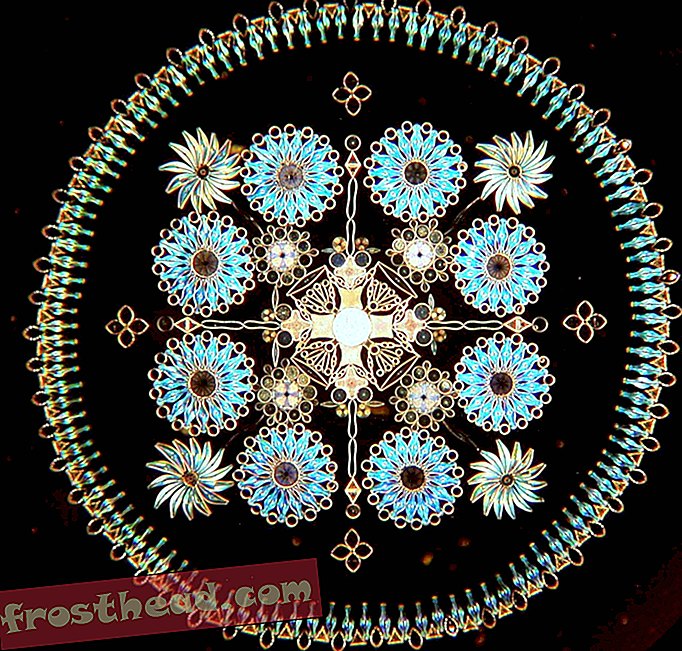（クラウス・ケンプ） 
（クラウス・ケンプ） 
（クラウス・ケンプ） ここでスケールの感覚を教えてください。 これらの配置はどれくらい小さいですか？
珪藻のサイズは5ミクロンから200ミクロンの範囲です。 ミクロンは、1000分の1ミリです。 100個のフォームの珪藻配列は、平均サイズのテキストの句読点の内側に収まります。
アートはどのように表示され、共有されましたか？
JDMöller（1844-1907）のようなプロの顕微鏡技師がしばしば手配しました。 それらは、顕微鏡写真を含む他のミニチュアの好奇心と一緒に、アミューズメントとして社交的な集まりでそれらを展示する裕福なアマチュア自然主義者に販売されました。
クラウス・ケンプはどのようにして珪藻学者になりましたか？
クラウスは、16歳で初めての珪藻の配置を見ました。すぐに夢中になり、見たものを再現しようと試みました。 クラウスが同等の取り決めをすることができるようになるまで、8年間の実験が必要でした。
彼は独学ですか？
クラウスは必然的に独学です。 ビクトリア時代の珪藻類は互いに競争しており、彼らの技術の秘密を正確に明らかにすることは決してありませんでした。彼らの方法はすべて一緒に墓に行きました。 信頼できる情報がないため、Klausは長年、接着剤の研究と実験を行い、珪藻をマウントするための完璧なソリューションを見つけました。 クラウスの特定の処方は現在彼にしか知られていないが、彼の妻は亡くなったらレシピをリリースするように指示されている。
彼はどこで珪藻を集めますか？ そして、具体的には、彼は何を探していますか？
珪藻は、水たまり、湖、川、海など、あらゆる水域で見つかる可能性があります。 クラウスは永遠にどこかの溝や海岸で新しい標本を探し回っており、世界中からサンプルを収集しています。 彼はまた、他の国からの標本を彼にしばしば提供する多くの外国の珪藻愛好家に対応しています。 クラウスはすべての珪藻に夢中ですが、マストグロイア属に特化しています-彼らは彼の真の情熱です。 クラウスはまた、いくつかの新しい種を発見しました。
ケンプは実際にどのように珪藻を配置しますか？ プロセスはどのように見えますか？
珪藻をきれいにした後、珪藻は接着剤でスライドガラスの上に置かれます。 その後、接着剤が許す限り、顕微鏡下で一定時間操作することができます。 クラウスは、非常に複雑なアレンジメントを作成するのに十分な時間をかけて数日間働くことができるユニークな接着剤の処方を持っています。 接着剤が固まったら、高屈折率の封入剤を加えます。 これにより、珪藻をより明確に見ることができます。 最後に、配置を保護するために別のスライドガラスが上部に配置されます。
あなたはこの種の仕事をするために少し怒っている必要がありますよね？
クラウスは、強迫観念が必要であることを自由に認めています。
これらの取り決めについて何が好きですか？
最高のアレンジが圧倒的だと思います。 形状、パターン、繰り返しの多様性と複雑さは、深いa敬の念を呼び起こします。 私はダーウィンを思い出さずにはいられません。「最も美しく、最も素晴らしい無限の形は進化してきました。そして進化しています」。
