数学を使用して究極のタフィーマシンを構築する科学| スミソニアン - 記事、歴史、革新、科学

私たちのほとんどは、観光客向けの遊歩道でタフィーを引く機械が回転しているのを見ると、甘い甘い砂糖を思い浮かべます。 Jean-Luc Thiffeaultは甘い甘い数学を考えています。ウィスコンシン大学マディソン校の応用数学者として、Thiffeaultはタフィーなどの材料の混合方法に特に興味を持っています。機械では、キャンディーを何度も何度も折り畳んで、空気を取り入れ、軽くて歯ごたえのある質感を生み出しています。引っ張られると、元のタフィーの長方形はますます引き伸ばされ、その長さは毎回同じ比率で指数関数的に増加します。そのストレッチ比は、Thiffeaultが興味を持っているものです。

関連性のあるコンテンツ

メルトプルーフチョコレート、3D印刷されたグミ、その他の魅力的なキャンディの特許

人がタフィーを引っ張るとき、彼らは一般的にキャンディーの塊を取り、フックの上に伸ばして、2つの端を一緒にします。次に、折りたたまれた部分を取り、フックの上で再度伸ばし、長さを2倍にします。言い換えると、「それを行う人間のやり方は2倍の倍率です」とThiffeault氏は言います。メカニカルプーラーはより良い結果を得ることができ、多くの場合、ストレッチファクターとして、より大きく、エキゾチックな無理数が得られます。

タフィープルは、トポロジダイナミクスとして知られる数学の抽象的な分野、基本的には数学空間での長期にわたる大規模な変化の研究によってモデル化できることがわかりました。（トポロジーという言葉がおなじみの場合、それは最近の今年のノーベル物理学賞の一部としてニュースにありました。）タフィー引きを説明する同じ数学も、より深刻なアプリケーションを持っています。コーヒーにクリームをかき混ぜるよりもタフィーを引くような方法で混合される粘性流体。「製薬業界のペーストなど、本当に粘り気のあるものをかき混ぜようとしているのなら、ただ振ることはできません」とThiffeaultは言います。「塗料を混ぜるようなものではありません。」

Thiffeaultは、タフィープルを粘性混合の例として長い間理解してきましたが、ごく最近になって、タフィープラーの数学的秘密を明らかにするためにタフィープラーの歴史を実際に調べました。その歴史的特許へのエクスカーションの結果は、7月にプレプリントサーバーarXivで発表された彼の最近の論文「タフィープーラーの数学的歴史」です。

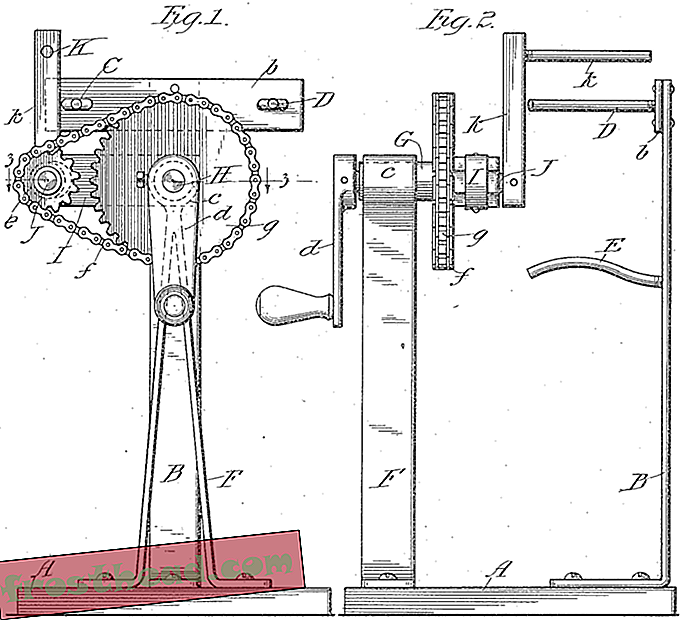$McCarthy1916_device.png$ Thiffeaultの研究に登場する1916年のタフィーマシン特許の画像。

具体的には、彼のタフィープラーディープダイビングにつながった領域は、疑似Anosovマッピングと呼ばれるものの研究です。 Pseudo-Anosovは、2次元形状が一方の方向に指数関数的に引き伸ばされ、もう一方の方向に縮むプロセスを記述するための凝った方法です。数学的には、疑似Anosovマッピングの研究は比較的新しいものです。「70年代と80年代に、人々は非常に一生懸命に例を見つけようとしていました」とThiffeault氏は言います。皮肉なことに、彼らはタフィープラーの特許でずっとそこにいた。「数学者はこの文献を決して見なかったので、彼らは彼らが存在したことを決して知らなかっただろう」と彼は言います。

彼はタフィープラーの特許を調べていたが、Thiffeaultは法廷闘争でつまずき、それが最高裁判所にまで及んだ。 1921年の事件で争点となったヒルドレス対マストラスは、タフィープラーの1900年特許がいかに広く解釈されるべきかでした。つまり、他の誰かによって作られた後のモデルはほんのわずかな改善でしたか、それとも別のデバイスでしたか？議論の重要な部分は、1900年の特許が1893年の前任者（おそらく製造されなかった）とどの程度異なるかでした。裁判所の意見は、ウィリアム・ハワード・タフト最高裁判所長官によって作成され、「位相ダイナミクスの鋭い把握を示しています」とThiffeaultは彼の記事に書いています。

裁判所は、2つのフックしか持たない以前のデバイスでは、効率的な菓子作りに必要な指数関数的な程度までタフィーを伸ばすことができなかったことを認識しました。タフトの意見は述べています：

キャンディーが2つだけの場合、キャンディーが他の2つのピンの間に保持されている間に再係合するための3番目のピンがなかったため、キャンディーのラッピングはありません。同心円での2本のピンの動きは、それをいくらか伸ばしてかき回すかもしれませんが、それは芸術の意味でそれを引っ張らないでしょう。

Thiffeaultは、「最高裁判所の意見は、何らかの急速な成長を生み出すには少なくとも3本の棒が必要であるという基本的な洞察を示しています。」

Thiffeault氏によると、現在使用されている標準タフィープラーは2本あり、1本は3本のロッド、もう1本は4本のロッドです。それらは同じストレッチファクターを持っています。これは、いわゆる銀比、1 +√2、または約2.414に関連しています。これは、より有名な黄金比のやや光度が低いいとこです。

2つの標準タフィープラーが銀の比率で伸びるという事実は、銀の比率が（正確な数学的意味で）最適であるため興味深いです。しかし、Thiffeaultは、ストレッチ要因を知っていても、さまざまなタフィープラーをランク付けすることはそれほど簡単ではないことを警告します。あるプラーのロッドが多く、他のプラーよりも初期状態に戻るのに時間がかかる場合や、より多くのトルクやより複雑なギアリングが必要な場合があります。そのため、数学はタフィープラーがどれだけうまく引っ張るかについてある程度の洞察を与えますが、完全なストーリーを語るわけではありません。

タッフィープラーに関するThiffeaultの研究は、彼と彼の学部生のAlex Flanaganにインスピレーションを与えて独自のモデルを構築しました。彼らは、ギアをあまり変更せずに効率を上げることができるかどうかを確認したいと考え、標準の4ロッドプーラーのギアリングに基づいて新しい6ロッドプーラーを作成しました。「それができたのは、今数学ができているからです」とThiffeaultは言います。彼らはコンピューター上で機械を広範囲にモデリングし、以前の発明者がしなければならなかった実際の物理デバイスでの多くの試行錯誤を回避することができました。まだプロトタイプに過ぎない6ロッドデバイスは、各サイクルで標準のプラーの約2倍のタフィーを伸ばします。

これまでのところ、タフィープラーのメーカーは、Thiffeaultの設計を最適化するためのアドバイスを得るために、Thiffeaultのドアを正確に叩いていませんでした。ガラス吹きに加えて、混合の最適化のための論理的な場所の1つは製薬業界です。結局のところ、ビタミンと薬物の混合には非常に高い品質管理が必要です。製造業者は「完全な混合に多額のお金を払おうとしています」。だからいつか、薬剤師は昔の献身的なタフィー屋に甘い叫び声をあげているかもしれません。

繰り返しますが、それは少しストレッチかもしれません。