今年の3月14日は定期的なPiデーではありません。 数学愛好家はどこでもイベントをUltimate Pi Dayとして祝います。これは、日付が最初の3桁ではなく、piの最初の5桁（3.1415）に対応するためです。 この数学的合流は、2115年3月14日に1世紀にわたって再び発生することはありません。
関連性のあるコンテンツ
- 世界は円でいっぱい
円の円周と直径の比として定義されるpi（ π ）は、超越数と無理数の両方です。つまり、2つの整数の比として書くことはできず、繰り返しパターンなしで無限に続きます。 無理数はPiだけではありません。たとえば、オイラー数（e）と黄金比（ φまたはphi）もあります。 しかし、その起源は簡単に説明できるため、それは魅力の源であり続けます、とメリーランドの宇宙望遠鏡科学研究所の天体物理学者、マリオ・リビオは言います。
「パイがどのように導出されるかは誰でも理解できます。 他のすべての数値はより複雑です。 たとえば、数字phiは線の特定の区分に関係し、数字eは対数が何であるかを知る必要があります」と書かれているLivioは書いています。
piのもう1つの大きな魅力は、数式に表示するための不思議なコツを持っていることです。その多くは、画像処理からGPSナビゲーションまでの日常のプロセスに重要です。 以下は、piを含む一般的に使用される数式のほんの一部のサンプルです。
フーリエ変換
フランスの数学者ジャン=バプティスト・ジョセフ・フーリエにちなんで名付けられたこの数学ツールは、信号を成分周波数に分解します。むしろ、音楽の和音を成分音に分解するようなものです。 基本的に、フーリエ変換は、音や光などの波ベースの信号を処理し、パターンを見つけるのに理想的です。 これにより、フーリエ変換は現代のデジタル世界の基本的なツールになります。
「人類がこれまでに開発した単一の最も重要なアルゴリズムと呼ばれています。 ニューヨーク市にある国立数学博物館の創設者でありディレクターであるグレン・ホイットニーは、次のように述べています。 フーリエ変換は、デジタル画像をクリーンアップしたり、ポップスターを自動調整したり、他のスターを周回する遠方の惑星を見つけるために常に使用されます。 このツールは、現在スマートフォンで標準となっている音声テキスト変換機能にとっても重要です。 「SiriまたはGoogle Nowを使用する場合、最初のステップの1つは、音声を受け取ってフーリエ変換を行うことです。フーリエ変換を見たときの母音の認識は、見たときよりもはるかに簡単です。元の信号そのものです」とホイットニーは言います。
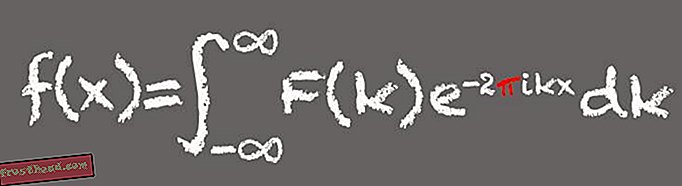（ビクトリアジャガードによるイラスト） 数式のコンポーネント部分または式の1つが正弦と余弦、および円の周りを移動する粒子によって作成された角度に関連付けられているため、Piはフーリエ変換に表示されます。 「円や角度を扱う数式があれば、円周率が現れても驚かないでしょう」とホイットニーは言います。
ハイゼンベルクの不確実性の原理
量子力学の柱の1つであるハイゼンベルクの不確定性の原理は、観測者が原子以下の粒子の位置と速度の両方を同時に知ることはできないと述べています。 代わりに、粒子の位置が正確にわかるほど、その速度について知ることができなくなります。
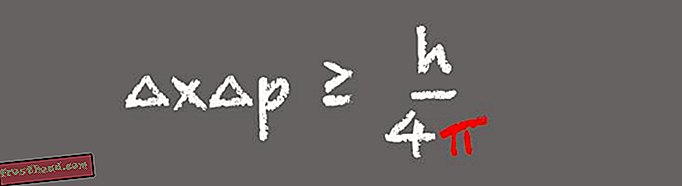（ビクトリアジャガードによるイラスト） ハイゼンベルクの不確定性原理におけるパイの出現は、式において、位置と運動量が互いのフーリエ変換であることに気づいたときに意味があります、とホイットニーは言います。 不確実性の原理は、光ファイバ通信システムにおける光の粒子または光子の挙動を説明するため、現代の世界では重要です。 「それは、光子の位置と運動量の両方を非常に正確に知ることができないということです。 ハイゼンベルグの不確実性の原則に違反する通信プロトコルを設計することはできません。なぜなら、それらは機能しないからです。」
ストークの法則
ストークの法則は、小さな球体、つまり3次元の円を特定の速度で粘性流体を通過させるのに必要な力を計算します。 地球科学から医学まで幅広い分野で応用されています。
（ビクトリアジャガードによるイラスト） 「この法則は、特に流体中の球体に対する粘性の影響に関するものです」と、ホイットニーは言います。 ストークの法則の実用的な使用に関しては、あなたの車よりももう探す必要はありません。 「何十年もの間、自動車用のオイルに適切な粘度があることを企業が確認する方法は、一連の試験球を文字通りオイルに落とし、液体を落ちるまでの時間を測定することでした」とホイットニーは言います。 今日、油の粘度を測定する最も一般的な方法は、毛細管粘度計と呼ばれるツールを使用し、球体は不要ですが、それでもセンチストークと呼ばれる測定単位で結果を報告します。
オイラーの式
スイスの数学者レナード・オイラーにちなんで名付けられた、piを含むこの式のバージョンは、数学で最も興味深い数個を1か所に集めています。
（ビクトリアジャガードによるイラスト） 「誰もがこれは信じられないほどだと思っています。 私たちが特別だと考えるこれらの数字はすべて、1つの美しい方程式に現れています」とLivioは言います。 この簡潔な公式は数学者にa敬の念を抱かせる可能性がありますが、方程式のより有用な形式はわずかに長くなります。
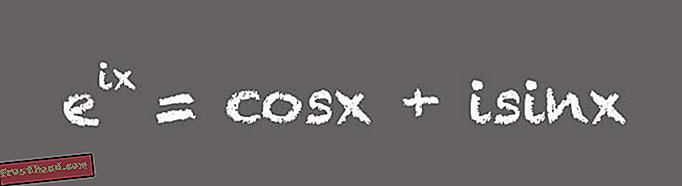（ビクトリアジャガードによるイラスト） オイラーの公式のこのパックされていないバージョンは信じられないほどのツールです、とホイットニーは言います。 たとえば、交流またはACを使用する電子機器の設計には重要です。 「拡張された形式のオイラーの公式は、AC回路の分析と設計に複雑な、または虚数を使用できることを意味します」とホイットニーは言います。 これは、交流回路では、電圧が時間とともに振動する量であるためです。たとえば、標準的な米国の電力供給では、通常1秒間に60回です。 「オイラーの公式の完全版は、振動現象をモデル化するための便利な速記法として複素数を使用する方法を教えています」とホイットニーは言います。
アインシュタインの場の方程式
アルバート・アインシュタインの場の方程式は、彼の一般相対性理論の核となる要素であり、質量とエネルギーからの重力が時空の曲率をどのように作り出すかを説明しています。
（ビクトリアジャガードによるイラスト） 「曲率はジオメトリに関係することを説明します。piの元の定義はジオメトリに由来するため、この式での外観はそれほど驚くことではありません」とLivio氏は言います。 宇宙がどのように機能するかについての基本的な真実を明らかにすることに加えて、一般相対性理論には多くの実用的な応用があります。 たとえば、航法に使用される全地球測位システムを構成する衛星は、エンジニアが理論で予測された時間膨張の影響を考慮しなければ、絶望的に互いに同期しなくなります。
